(Click here for a Postscript version of this page).
It is of great importance to solve equations of the form
|
in many applications in Mathematics, Physics, Chemistry, ... and of course in the computation of some important mathematical constants or functions like square roots. In this essay, we are only interested in one type of methods : the Newton's methods.
Around 1669, Isaac Newton (1643-1727) gave a new algorithm [3] to solve a polynomial equation and it was illustrated on the example y3-2y-5=0. To find an accurate root of this equation, first one must guess a starting value, here y » 2. Then just write y=2+p and after the substitution the equation becomes
|
Because p is supposed to be small we neglect p3+6p2 compared to 10p-1 and the previous equation gives p » 0.1, therefore a better approximation of the root is y » 2.1. It's possible to repeat this process and write p=0.1+q, the substitution gives
|
hence q » -0.061/11.23=-0.0054... and a new approximation for y » 2.0946... And the process should be repeated until the required number of digits is reached.
In his method, Newton doesn't explicitly use the notion of derivative and he only applies it on polynomial equations.
A few years later, in 1690, a new step was made by Joseph Raphson (1678-1715) who proposed a method [6] which avoided the substitutions in Newton's approach. He illustrated his algorithm on the equation x3-bx+c=0, and starting with an approximation of this equation x » g, a better approximation is given by
|
Observe that the denominator of the fraction is the opposite of the derivative of the numerator.
This was the historical beginning of the very important Newton's (or sometimes called Newton-Raphson's) algorithm.
The method was then studied and generalized by other mathematicians like Simpson (1710-1761), Mourraille (1720-1808), Cauchy (1789-1857), Kantorovich (1912-1986), ... The important question of the choice of the starting point was first approached by Mourraille in 1768 and the difficulty to make this choice is the main drawback of the algorithm (see also [5]).
Nowadays, Newton's method is a generalized process to find an accurate root of a system (or a single) equations f(x)=0. We suppose that f is a C2function on a given interval, then using Taylor's expansion near x
|
and if we stop at the first order (linearization of the equation), we are looking for a small h such as
|
giving
|
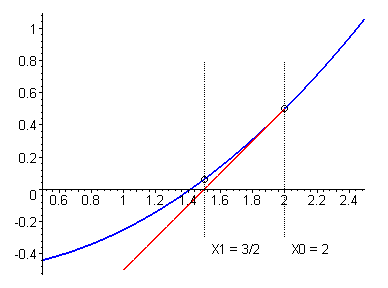
The Newton iteration is then given by the following procedure: start with an initial guess of the root x0, then find the limit of recurrence:
|
and Figure 1 is a geometrical interpretation of a single iteration of this formula.

Unfortunately, this iteration may not converge or is unstable (we say chaotic sometimes) in many cases. However we have two important theorems giving conditions to insure the convergence of the process (see [2]).
Theorem 1
Let x* be a root of f(x)=0, where f is a C2function on an
interval containing x*, and we suppose that | f¢(x*)| > 0, then Newton's iteration will converge to x* if the
starting point x0 is close enough to x*.
Theorem 2
(Kantorovich). Let f be a C2 numerical function from an open interval
I of the real line, let x0 be a point in this interval, then if there
exist finite positive constants (m0,M0,K0) such as
and if h0=2m0M0K0 £ 1,Newton's iteration will converge to a
root x* of f(x)=0, and
ê
ê
1
ê
ê
< m0,
ê
ê
f(x0)
ê
ê
< M0,
| f¢¢(x0)|
< K0,
| xn-x*| < 21-nM0h02n-1.
Newton's iteration may be seen as a first order method (or linearization method), it's possible to go one step further and write the Taylor expansion of f to a higher order
|
and we are looking for h such as
|
we take the smallest solution for h (we have to suppose that f¢(x) and f¢¢(x) are non zero)
|
It's not necessary to compute the square root, because if f(x) is small, using the expansion
|
h becomes
|
The first attempt to use the second order expansion is due to the astronomer E. Halley (1656-1743) in 1694.
The previous expression for h, allows to derive the following cubic iteration (the number of digits triples at each iteration), starting with x0
|
This procedure is given in [1]. It can be efficiently used to compute the inverse or the square root of a number.
Another similar cubic iteration may be given by
|
sometimes known as Halley's method. We may also write it as
|
Note that if we replace (1-a)-1 by 1+a+O(a2), we retrieve Householder's iteration.
Under some conditions of regularity of f and it's derivative, Householder gave in [1] the general iteration
|
where p is an integer and (1/f)(p) is the derivative of order p of the inverse of the function f. This iteration has convergence of order (p+2). For example p=0 has quadratic convergence (order 2) and the formula gives back Newton's iteration while p=1 has cubical convergence (order 3) and gives again Halley's method. Just like Newton's method a good starting point is required to insure convergence.
Using the iteration with p=2, gives the following iteration which has quartical convergence (order 4)
|
Another idea is to write
|
where hn=-f(xn)/f¢(xn) is given by the simple Newton's iteration and (a2n,a3n,...) are real parameters which we will estimate in order to minimize the value of f(xn+1):
|
we assume that f is regular enough and hn+a2nhn2/2!+a3nhn3/3!+... is small, hence using the expansion of f near xn
|
and because f(xn)+hnf¢(xn)=0, we have
|
A good choice for the ain is clearly to cancel as many terms as possible in the previous expansion, so we impose
|
with, for the sake of brevity, the notation fn(k)=f(k)(xn). The formal values of the ain may be computed for
much larger values of i. Finally the general iteration is
|
For example, if we stop at a3n and set a4n=a5n=...=0, we
have the helpful quartic modified iteration (note that this
iteration is different than the previous Householder's quartic method)
|
and if we omit a3n, we retrieve Householder's cubic iteration.
It's also possible to find the expressions for (a4n,a5n,a6n,a7n,...), and define quintic, sextic, septic, octic ... iterations.
In the essay on the square root of two, some applications of those methods are given and also in the essay on how compute the inverse or the square root of a number. Here let's compare the different iterations on the computation of the Golden Ratio
|
First we write j = 1/2+x and x=Ö5/2 is root of the equation
|
then, it's convenient to set hn=1-4/5×xn2, we have the 5 algorithms, deduced from the general previous methods (left as exercise!), with respectively quadratic, cubic, quartic, sextic and octic convergence :
|
Starting with the initial value x0=1.118, the first iteration becomes respectively
|
and one more step gives for x2 respectively 17, 39, 69,154 and 273 good digits. If we iterate just three more steps, x5 will give respectively 139, 1049, 4406, 33321 and 140053 correct digits ... Observe that hn tends to zero as n increases which may be used to accelerate the computations and the choice of the best algorithm depends on your implementation (algorithm used for multiplication, the square, ...)
Newton's method may also be used to find a root of a system of two or more non linear equations
|
where f and g are C2functions on a given domain. Using Taylor's expansion of the two functions near (x,y) we find
|
and if we keep only the first order terms, we are looking for a couple (h,k) such as
|
hence it's equivalent to the linear system
|
The (2×2) matrix is called the Jacobian matrix (or Jacobian) and is sometimes denoted
|
(it's generalization as a (N×N) matrix for a system of N equations and N variables is immediate) . This suggest to define the new process
|
starting with an initial guess (x0,y0) and under certain conditions (which are not so easy to check and this is again the main disadvantage of the method), it's possible to show that this process converges to a root of the system. The convergence remains quadratic.
Example 3
We are looking for a root near (x0=-0.6,y0=0.6) of the following
system
here the Jacobian and its inverse become
and the process gives
Depending on your initial guess Newton's process may converge to one of the
three roots of the system:
and for some values of (x0,y0) the convergence of the process may be
tricky! The study of the influence of this initial guess leads to aesthetic
fractal pictures.
f(x,y)
=x3-3xy2-1
g(x,y)
=3x2y-y3,
J(xn,yn)
=3
æ
ç
è
xn2-yn2
-2xnyn
2xnyn
xn2-yn2
ö
÷
ø
J-1(xn,yn)
=
1
æ
ç
è
xn2-yn2
2xnyn
-2xnyn
xn2-yn2
ö
÷
ø
x1
=-0.40000000000000000000,y1=0.86296296296296296296
x2
=-0.50478978186242263605,y2=0.85646430512069295697
x3
=-0.49988539803643124722,y3=0.86603764032215486664
x4
=-0.50000000406150565266,y4=0.86602539113638168322
x5
=-0.49999999999999983928,y5=0.86602540378443871965
...
(-1/2,Ö3/2),(-1/2,-Ö3/2),(1,0),