(Click here for a Postscript version of this page and here for a pdf version)
It's a very old fact (Euclid 325-265 B.C., in Book IX of the Elements) that the set of primes is infinite and a much more recent and famous result
(by Jacques Hadamard (1865-1963) and Charles-Jean de la Vallee Poussin
(1866-1962)) that the density of primes is ruled by the law
|
This approximation may be usefully replaced by the more accurate
logarithmic integral Li(n):
|
However among the deeply studied set of primes there is a famous and fascinating subset for which very little is known and has generated some famous conjectures: the twin primes (the term prime pairs was used before [5]).
Definition 1 A couple of primes (p,q) are said to be twins if q=p+2. Except for the couple (2,3), this is clearly the smallest possible distance between two primes.
Example 2 (3,5),(5,7),(11,13),(17,19),(29,31),...,(419,421),... are twin primes.
As for the set of primes the most natural question is wether the set of twin primes is finite or not. But unlike prime numbers for which numerous and elementary proofs exist [10], the answer to this natural question is still unknown for twin primes ! Today, this problem remains one of the greatest challenge in mathematics and has occupied numbers of mathematicians. Of course, as we will see, there are some empirical and numerical results suggesting an answer and most mathematicians believe that there are infinitely many twin primes.
In 1849, Alphonse de Polignac (1817-1890) made the general conjecture that there are infinitely many primes distant from 2k. The case for which k=1 is the twin primes case.
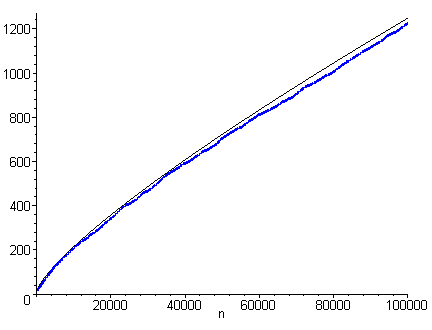
It's now natural to introduce the twin prime counting function p2(n) which is the number of twin primes smaller than a given n.
Using huge table of primes (Glaisher 1878 [5], before computer age, enumerated p2(105)) and with intensive computations during modern period (Shanks and Wrench 1974 [12], Brent 1976 [1], Nicely 1996-2002 [9], Sebah 2001-2002 [11], see also [10]) it's possible to compute the exact values of p2(n) for large n and its conjectured approximation 2C2Li2(n) (see next section for the definition).
The following array includes the relative error e (in %) between the approximation and the real value.
| n | p2(n) | 2C2Li2(n) | e |
| 10 | 2 | 5 | 150.00 |
| 102 | 8 | 14 | 75.00 |
| 103 | 35 | 46 | 31.43 |
| 104 | 205 | 214 | 4.39 |
| 105 | 1224 | 1249 | 2.04 |
| 106 | 8169 | 8248 | 0.97 |
| 107 | 58980 | 58754 | -0.38 |
| 108 | 440312 | 440368 | 0.013 |
| 109 | 3424506 | 3425308 | 0.023 |
| 1010 | 27412679 | 27411417 | -0.0046 |
| 1011 | 224376048 | 224368865 | -0.0032 |
| 1012 | 1870585220 | 1870559867 | -0.0013 |
| 1013 | 15834664872 | 15834598305 | -0.00042 |
| 1014 | 135780321665 | 135780264894 | -0.000042 |
| 1015 | 1177209242304 | 1177208491861 | -0.000064 |
| 1016 | 10304195697298 | 10304192554496 | -0.000031 |
At present time (2002), Pascal Sebah has reached p2(1016) and his values are confirmed by Thomas Nicely up to p2(4.1015) who used an independent approach and implementation.
Because the most convenient (in fact the only available) way to compute p2(n) is to find all twin primes and just count them, it's of great importance to improve as much as possible such an algorithm. All known methods use variations on the historical Eratosthenes sieve.
In order to accelerate the sieve, a possible idea is to represent integers modulo a base m, so that any integer has the form mk+r with 0 £ r < m. Primes numbers are such as m and r are relatively primes and for any value of m, there are f(m) numbers r which are prime with m (this is the definition of Euler's f totient function).
Modulo 6
For example modulo 6 all integers have one of the form
|
|
|
This allows to sieve a proportion of only f(m)/m=2/6 or 33.3% of all the numbers.
Modulo 30
The same kind of approach modulo 30 gives for candidates
|
But remember that we are only trying to sieve twin primes hence are left only
the candidate couples
|
This suggest to introduce the function f2(m) which is the number of
pairs of integer 0 £ r < m such as r and r+2 are relatively prime with
m. We observe from the last two examples that
|
Example
Let's illustrate this on a numerical example. The enumeration of twin primes
modulo 30 up to 1010 gives, respectively, for each of the 3 previous
couples:
|
|
|
|
It's interesting to observe that the contribution to the enumeration of the twin primes of each couple is almost equivalent. This was also observed during all numerical estimations for other modulo like 210, 2310, 30030, ... [11].
This result is well known when enumerating just prime numbers but may be conjectured for twin primes.
Other modulo
In this table we show the proportion 2f2(m)/m of integer to sieve in order to count twin primes as a function of the modulo m:
| m | f2(m) | % |
| 2 | . | 50.0 |
| 6 | 1 | 33.3 |
| 30 | 3 | 20.0 |
| 210 | 15 | 14.3 |
| 2310 | 135 | 11.7 |
| 30030 | 1485 | 9.9 |
| 510510 | 22275 | 8.7 |
The smallest ratios are obtained for values of m which are the product of the first primes (2#=2,3#=2×3,5#=2×3×5,7#=2×3×5×7,...), that is the first values of the primorial # function. For example in [11], the sieves were made modulo 30030 and 510510, therefore less than 10% of the set of integers were considered by the algorithm. In some others implementations sieves modulo 6 or 30 are used.
Based on heuristic considerations, a law (the twin prime conjecture) was developed, in 1922, by Godfrey Harold Hardy (1877-1947) and John Edensor Littlewood (1885-1977) to estimate the density of twin primes.
According to the prime number theorem the probability that a number
n is prime is about 1/log(n), therefore, if the probability that n+2 is
also prime was independent of the probability for n, we should have the
approximation
|
Conjecture 3
[Twin prime conjecture]For large values of n, the two following equivalent
approximations are conjectured
| (1) |
| (2) |
Note that C2 is the twin prime constant and is defined by
|
This last constant occurs in some asymptotic estimations involving primes and it's interesting to observe that it may be estimated using properties of the Riemann Zeta function to thousand of digits (Sebah computed it to more than 5000 digits).

Remark 4
The function Li2(n) occuring in (1) may be related to the
logarithmic integral Li(n) by the trivial relation
|
In fact, Hardy and Littlewood made a more general conjecture on the primes separated by a gap of d. A natural generalization of the twin primes is to search for primes distant of d=2k (which should be infinite for any d according to Polignac's conjecture). The case d=2 is the twin primes set, d=4 forms the cousin primes set, d=6 is the sexy primes set, ...
If we denote pd(n) the number of primes p £ n such as p+d is also
prime (observe that here p and p+d may not be consecutive),
Hardy-Littlewood's conjecture states (in [7]) that for
d ³ 2:
|
|
The first values of the function Rd are
| d | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| Rd | 1 | 1 | 2 | 1 | 4/3 | 2 | 6/5 | 1 | 2 | 4/3 |
According to this conjecture the density of twin primes is equivalent to the density of cousin primes. For example, the exact computed values up to 1012 are:
p2(1012) =1870585220
p4(1012) =1870585458,
which can be compared to the predicted value 1870559867 by the conjecture.
Marek Wolf has studied the function
|
Euler's constant
It's very natural to understand the nature of the harmonic numbers
|
|
Mertens' constant
The next step is to take in account only the primes numbers in the sum that
is
|
|
Therefore the sum diverges (this was also observed by Euler) but at the very low rate log(log(p)) and M is the interesting Mertens' constant which may be evaluated to much less digits than g, say a few thousands.
Brun's Constant
In the last step we only take in account the twin primes less than p in the
sum
|
Theorem 5 The sum of the inverse of the twin primes converges to a finite constant B2.
We write this result as
|
Note that this theorem doesn't answer to the question of the infinitude of twin primes, it just says that the limit exists (and may or may not contains a finite number of terms !). The proof is rather complex and based on a majoration of the density of twin primes ; a more modern one may also be found in [8].
Unlike Euler's constant or Mertens' constant, Brun's constant is one of the hardest to evaluate and we are not even sure to know 9 digits of it. By mean of very intensive computations, we only have guaranteed minorations !
In the following table we have try to estimate this constant by computing the partial sums B2(p) up to different values of p.
| p | B2(p) |
| 102 | 1.330990365719... |
| 104 | 1.616893557432... |
| 106 | 1.710776930804... |
| 108 | 1.758815621067... |
| 1010 | 1.787478502719... |
| 1012 | 1.806592419175... |
| 1014 | 1.820244968130... |
| 1015 | 1.825706013240... |
| 1016 | 1.830484424658... |
From this, we observe that the convergence is extremely slow and irregular. If we expect to find even just a few digits, we have to make some assumptions.
An easy consequence of the twin prime conjecture is that we may write the
numbers B2(p) as (see [4] and [9])
|
|
Let's take a look to numerical values:
| p | B2*(p) |
| 102 | 1.904399633290... |
| 104 | 1.903598191217... |
| 106 | 1.901913353327... |
| 108 | 1.902167937960... |
| 1010 | 1.902160356233... |
| 1012 | 1.902160630437... |
| 1014 | 1.902160577783... |
| 1015 | 1.902160582249... |
| 1016 | 1.902160583104... |
which suggest that the value of B2 should be around 1.902160583... (a similar value was first proposed by Nicely after intensive computations and checked later by Sebah, see [9] and [11]).
The relation
|

The intersection of the line with the vertical axis (that is p=¥) is Brun's constant if the twin prime conjecture is valid. And according to this line the direct estimation B2(p) should reach 1.9 not before the value p ~ 10530 which is far beyond any computational project !
There is a result from Clement (1949, [3]) which permits to see if a couple (p,p+2) is a twin primes pair. This theorem extends Wilson's famous theorem on prime numbers.
Theorem 6
Let p ³ 3, the integers (p,p+2) form a twin primes pair if and only if
|
Example 7 For p=17, 4( (p-1)!+1) = 83691159552004 º 306 mod 323 and -p º 306 mod 323, therefore (17,19) is a twin prime pair.
The huge value of the factorial makes this theorem of no practical use to find large twin primes.
Today, thanks to modern computers, a lot of huge twin primes are known. Many of those primes are of the form k×2n±1 because there are efficient primality testing algorithms for such numbers when k is not too large.
The following theorem due to the French farmer François Proth (1852-1879) may be used.
Theorem 8
[Proth's theorem - 1878]Let N=k.2n+1 with k < 2n, if there is an
integer a such as
|
To help finding large pairs, an idea is to take a value for n and then to start a sieve in order to reduce the set of possible values for the k. It should take a few hours to find twin primes with a few thousands digits.
For example the following numbers are twin prime pairs (some are given from
[10]):
|
The last one is a twin primes pair of more than 32000 digits !