(Click here
for a Postscript version of this page and here
for a pdf version)
Up to the Seventeenth Century, approximations of p were obtained by mean of geometrical considerations. Most of the methods were dealing with regular polygons circumscribed about and inscribed in the circle. The perimeter or the area of those polygons were calculated with elementary geometrical rules.
During this period the notation p was not used and it was not yet a constant but just a geometrical ratio or even just implicit.
In one of the oldest mathematical text, the Rhind papyrus (from
the name of the Egyptologist Henry Rhind who purchased this document in 1858
at Luxor), the scribe Ahmes copied, around 1650 B.C.E., eighty-five
mathematical problems. Among those is given a rule, the problem 48,
to find the area of a circular field of diameter 9: take away 1/9 of
the diameter and take the square of the remainder. In modern notation, it
becomes
|
|
This accuracy is astonishing for such ancient time. See [4] for a possible justification of this value.
On a Babylonian cuneiform tablet from Susa, about 2000 B.C.E., and
discovered in 1936, the ratio of the perimeter of the circle to its diameter
was founded to be
|
The famous treatise On the measurement of the Circle from the Greek
mathematician and engineer Archimedes of Syracuse (287-212 B.C.E.) is a
major step in the knowledge of the circle properties. Among those are given
the following numerical bounds for p
|
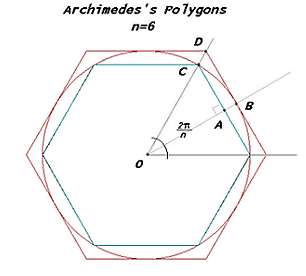
The proof uses a recursive algorithm starting with two regular hexagons (see figure 1), one is circumscribed and the other is inscribed. Archimedes then subdivides both polygons by 2, so the number of sides of the polygons is 6.2n (respectively 6,12,24,48,96 sides in his computations). The perimeters of the last polygons gives the announced bounds.

In modern notations this gives, for the circumscribed polygons, the
following recursive sequence (where un is half the length of the side
of the polygon and vn the distance from a vertex of the polygon to the
center of the circle)
|
We may observe that Archimedes needed to compute square roots to achieve his computation, and in particular he used a good approximation of Ö3 » 265/153 (this value is one of the partial quotients of the continued fraction of Ö3). The upper bound founded by Archimedes is given with n=4.
Now we observe the value of the first iterates of this sequence:
|
The same kind of iteration may be written for the inscribed polygons. Archimedes method is the first known algorithm, in theory, to compute p at a desired accuracy.
For example, p16 is a nine digits approximation and it is the perimeter of a polygon of 393216 sides. This approximation was given much later than Archimedes by François Viète (1540-1603) after a long calculation. He gave the bounds [9]:
|
Using trigonometric functions (unknown to Archimedes), it's easy to show
that the perimeter of the circumscribed polygon with n sides on a circle
of radius r is given by
|
|
It follows the bounds for p
|
|
If we observe that, when n is large,
|
|
|
|
See [7] for other accelerations of this method.
In 1800, Johann Friedrich Pfaff (1765-1825) gave a modern and analytical
formulation of the previous geometric iteration. Let an and bn be
respectively the length of the circumscribed and inscribed regular polygon
with 6.2n sides, then starting with a0=2Ö3,b0=3 and
|
|
If we set an=1/un and bn=1/vn the iteration
becomes (starting with a0=1/(2Ö3),b0=1/3)
|
|
It's interesting to note that this formulation is not very far from the AGM iteration which is one of the recent and very efficient methods used to compute many digits of p.
Here are some other approximations computed by various mathematicians and mostly by mean of polygons:
A very complete outline of the history of p is given in [8] and a more modern one are in [2] and [3].